La espiral de Teodoro y los números irracionales

el

La espiral de Teodoro, también llamada caracola pitagórica, espiral pitagórica, espiral de Einstein o espiral de raíces cuadradas (será por nombres) es una espiral formada por triángulos rectángulos contiguos, atribuida a Teodoro de Cirene (465 a. C. – 398 aC)

Alumno de Pitágoras, la espiral se genera a partir de un triángulo rectángulo isósceles de catetos unidad, formando sucesivos triángulos rectángulos con sendos catetos formados por la hipotenusa anterior y la unidad.

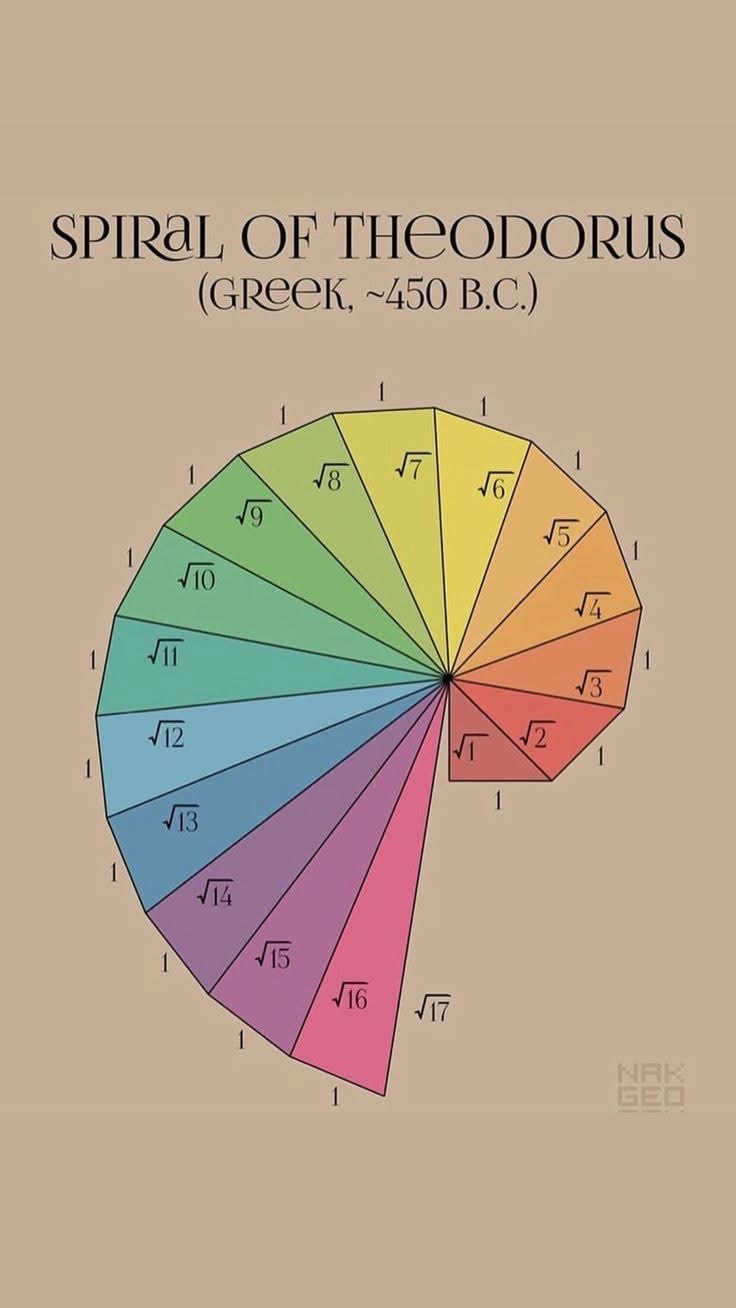
Teodoro finalizó su espiral en el triángulo rectángulo de hipotenusa √17. Si la espiral continua con la construcción de infinitos triángulos, surgen muchas características y propiedades interesantes.

Hipotenusas

Cada una de las hipotenusas de los triángulos hi (que se corresponden con los radios de la espiral) dan la raíz cuadrada para el número naturalconsecutivo, con h1 = √2, h2 = √3, h3= √4=2 y así sucesivamente.

Vértices y radios

En 1958, Erich Teuffel demostró que no hay dos hipotenusas de los triángulos con los que se construye la hélice, que coincidan sobre el mismo radio. Además, si los catetos que miden una unidad de longitud se prolongan mediante una línea recta, nunca pasarán a través de ningún otro de los vértices de la espiral.

Crecimiento

Ángulos

Si φn es el ángulo del n-ésimo triángulo (o segmento de espiral), entonces:

{\displaystyle \tan \left(\varphi _{n}\right)={\frac {1}{\sqrt {n}}}.}

Por lo tanto, el crecimiento del ángulo φn del siguiente triángulo n es:[5]​

{\displaystyle \varphi _{n}=\arctan \left({\frac {1}{\sqrt {n}}}\right).}

La suma de los ángulos de los primeros k triángulos, se designa ángulo total φ(k) del k triángulo, y es igual a:

{\displaystyle \varphi \left(k\right)=\sum _{n=1}^{k}\varphi _{n}=2{\sqrt {k}}+c_{2}(k)}

con

{\displaystyle \lim _{k\to \infty }c_{2}(k)=-2.157782996659\ldots .}

Un triángulo o sección de la espiral

Radios

El crecimiento del radio de la espiral hasta un cierto triángulo n es

{\displaystyle \Delta r={\sqrt {n+1}}-{\sqrt {n}}.}

Desarrollo y Área

Dado que el incremento del radio en cada vuelta tiende a Π, a medida que se incrementa el número de vueltas, la longitud de la espira tiende a crecer en cada vuelta:

{\displaystyle \Delta l=2\Pi \Delta r=2\Pi ^{2}=19.7392088022...}

y el área de cada espira, tiende a incrementarse respecto a la anterior en:

{\displaystyle \Delta S=\Delta l\Delta r=2\Pi ^{2}\Pi =2\Pi ^{3}=62.0125533606...}

Espiral de Arquímedes

La espiral de Teodoro frente a la espiral de Arquímedes

La espiral de Teodoro se aproxima a una espiral de Arquímedes con la expresión:

{\displaystyle \,r=1.078891298+(1/2)\theta }

La distancia entre dos brazos consecutivos de la espiral de Arquímedes es proporcional a pi. Cuando el número de giros de la espiral de Teodoro tiende a infinito, la distancia entre dos brazos de espiral consecutivos se aproxima rápidamente a π.

La siguiente tabla muestra la distancia media entre cada brazo de la espiral de Teodoro y el anterior, aproximándose a π:

Revolución o brazo No.:Promedio calculado de la distancia entre un brazo y el anteriorExactitud en comparación a π

23.159203799.44255%
33.144345599.91245%
43.1442899.91453%
53.14239599.97447%
→ ∞→ π→ 100%

Como puede verse, después de la quinta vuelta de la espiral, la distancia tiene un exactitud aproximada de 99.97% con respecto al valor de π.

Comentarios

Publicar un comentario